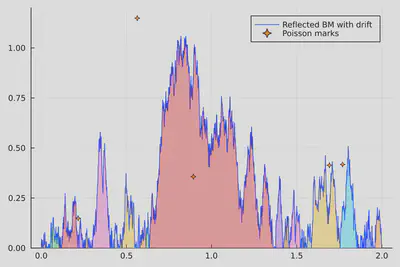
Simulations for the (augmented) multiplicative coalescent
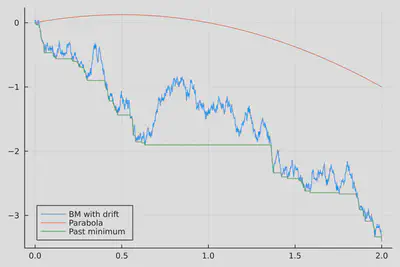
$$ B_t(s) = W_t(s) - \inf_{0 \leq u \leq s} W_t(u),$$ where $ W_t(s) = W(s) - \frac{1}{2}s^2 + t s $.
-
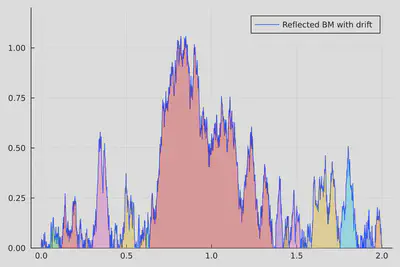
$X_i(t)$: $i$th largest excursion of $B_t(\cdot)$ above zero,
-
$\big( \pmb{X}(t), t \ge 0 \big) $ is a realization of an eternal multiplicative coalescent.
- $\Lambda$: homogeneous Poisson point process on $\mathbb{R}_+^2$,
- $X_i(t)$: $i$th largest excursion above zero,
- $Y_i(t)$: nb. of marks below the curve during the $i$th largest excursion.
$\big( (\pmb{X}(t), \pmb{Y}(t)), t \ge 0 \big) $ is a realization of an eternal augmented multiplicative coalescent.