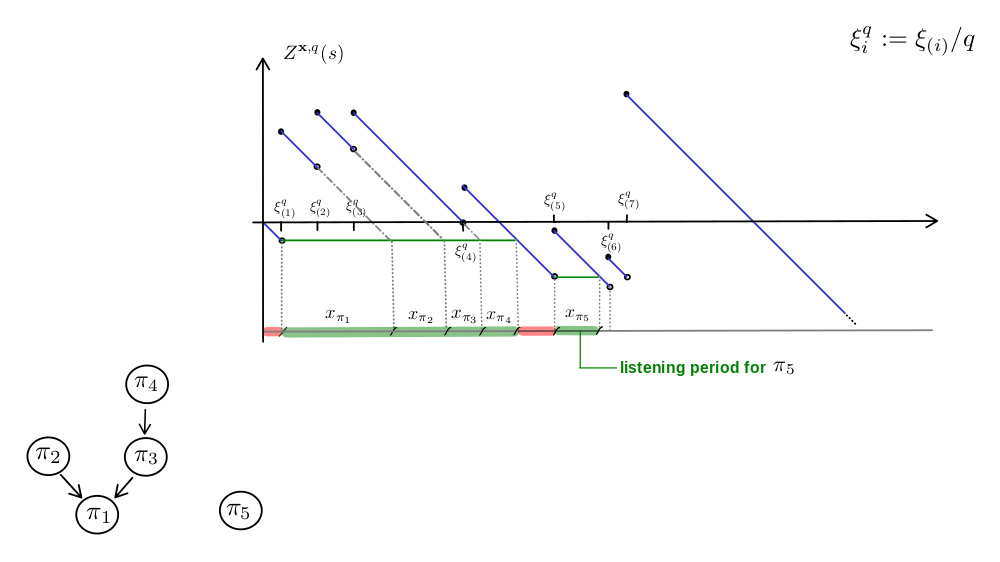
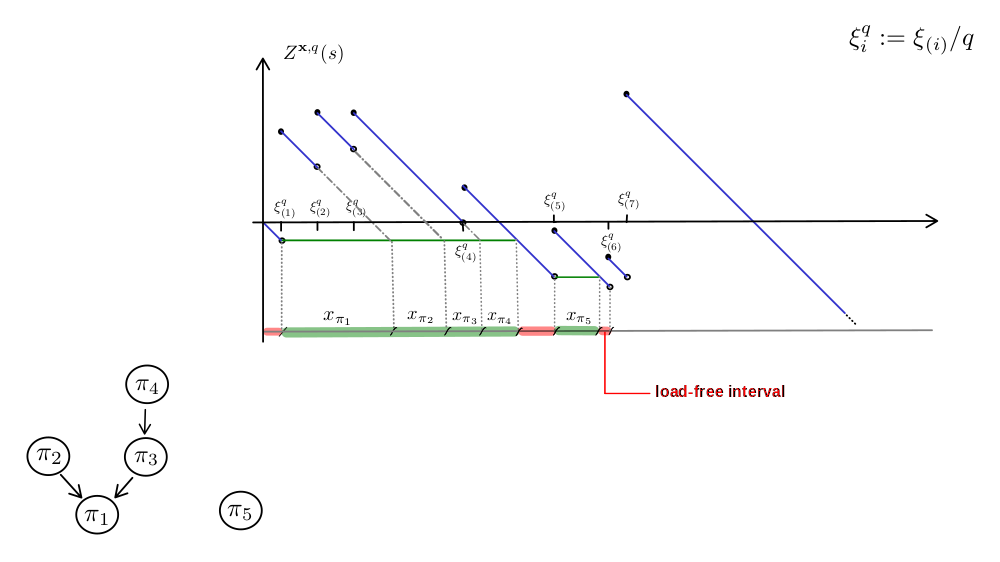
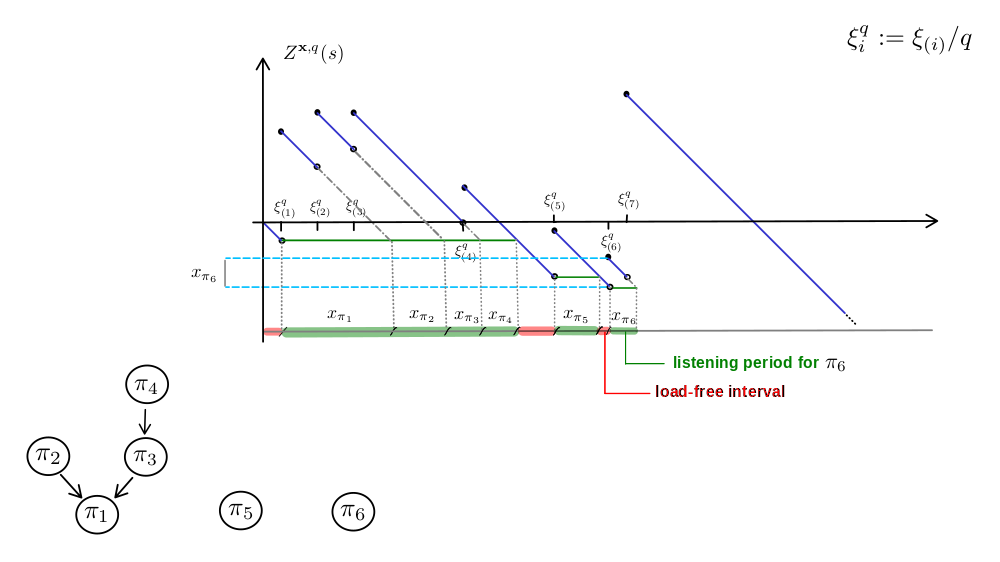
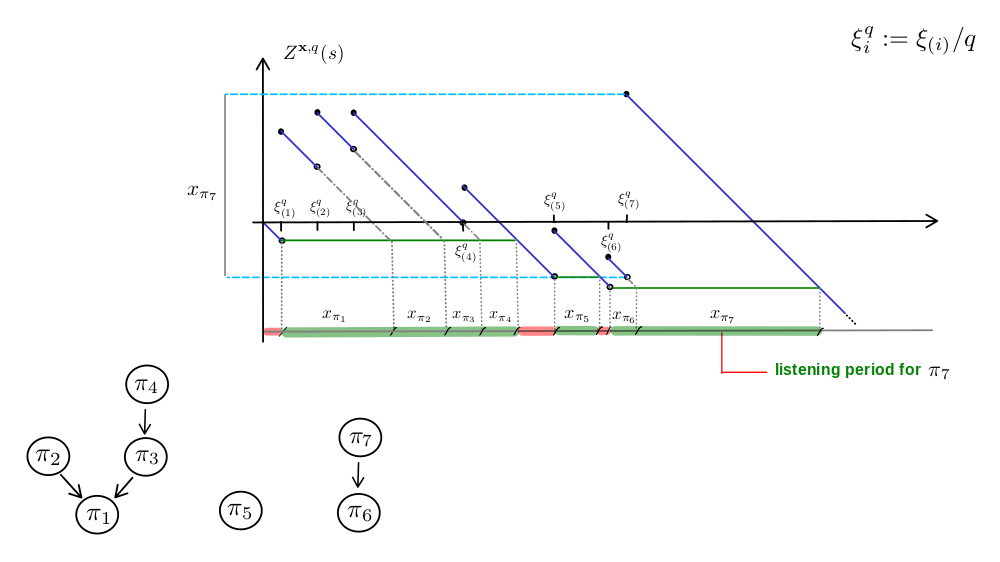
Chalk talk
Josué Corujo
Instituto Gulbenkian de Ciência, 6th June 2023
Digression: theorem-proof and scientific modelling mathematics
To ask ‘‘what is known’’ in this subject leads inexorably to philosophical issues concerning pure and applied mathematics… I call this scientific modelling (SM) mathematics, as opposed to theorem-proof (TP) mathematics, which is the style of all ‘‘pure’’ and much of what is called ‘‘applied’’ mathematics. In SM mathematics, models may be incompletely or inconsistently specified; the focus is on obtaining conclusions about the model, allowing appeals to physical realism, unquantified approximations, and arguments by analogy. In TP mathematics, one is supposed to have explicit assumptions and conclusions, as well as a rigorous argument linking them.
- David Aldous (Bernoulli 5(1), 1999, 3-48)
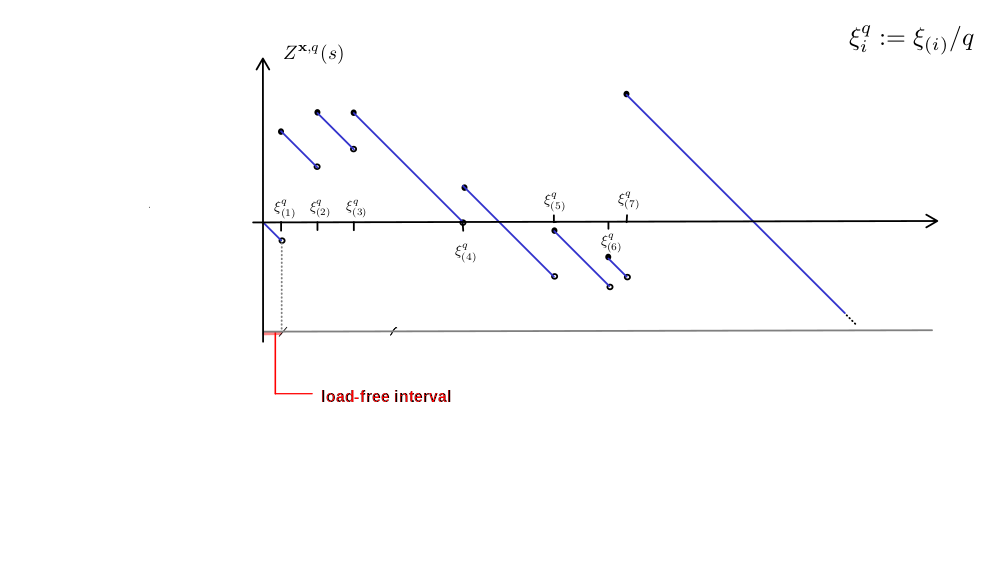
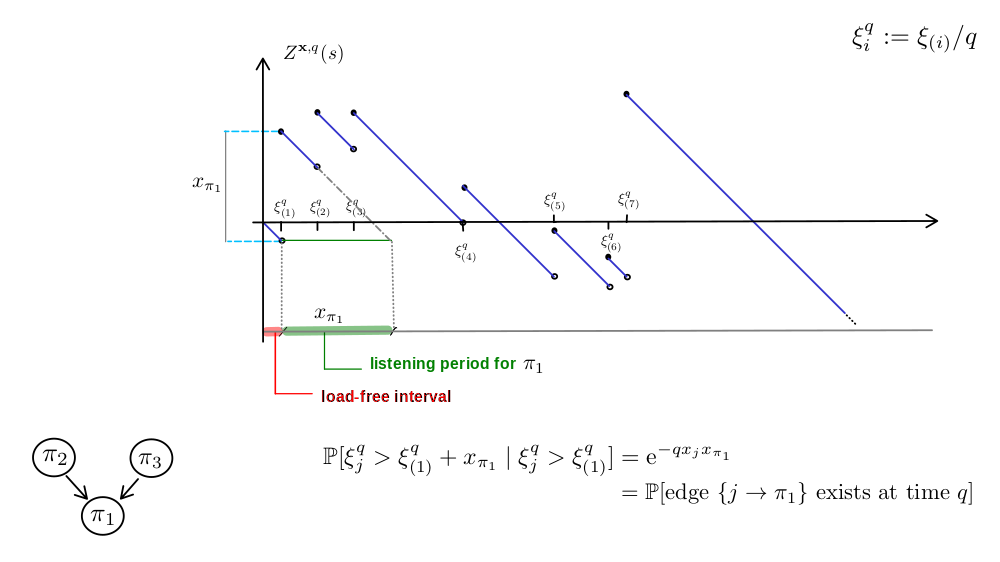
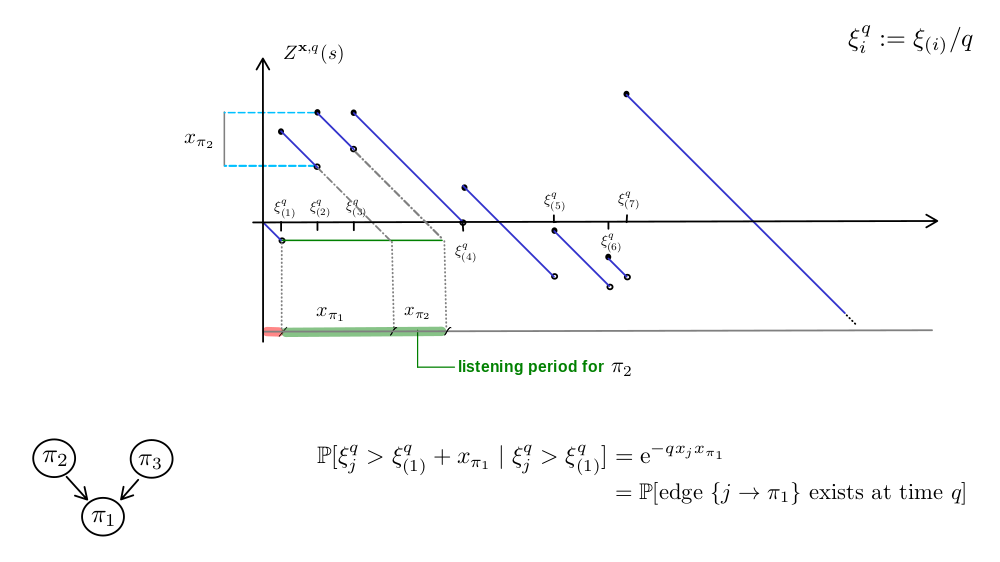
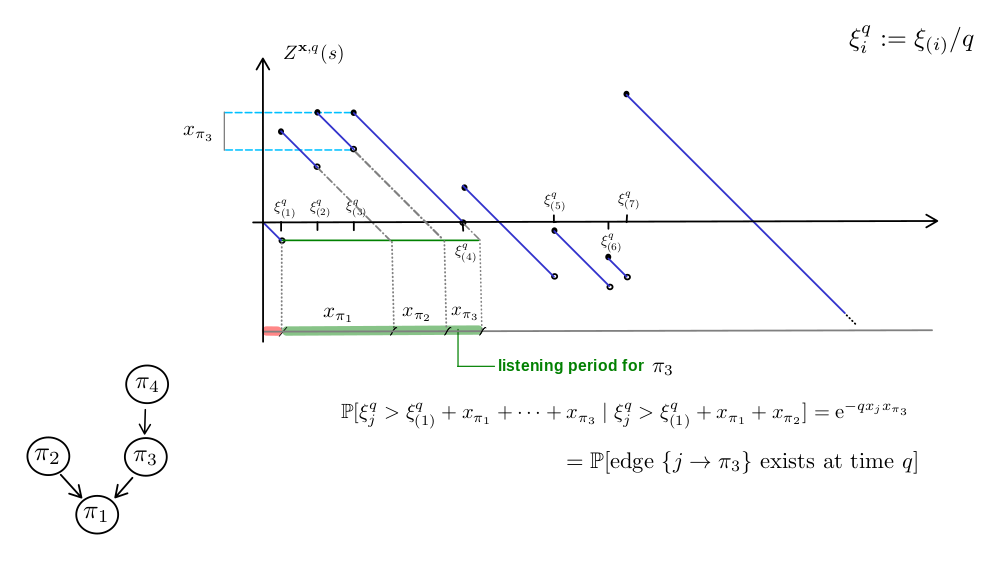
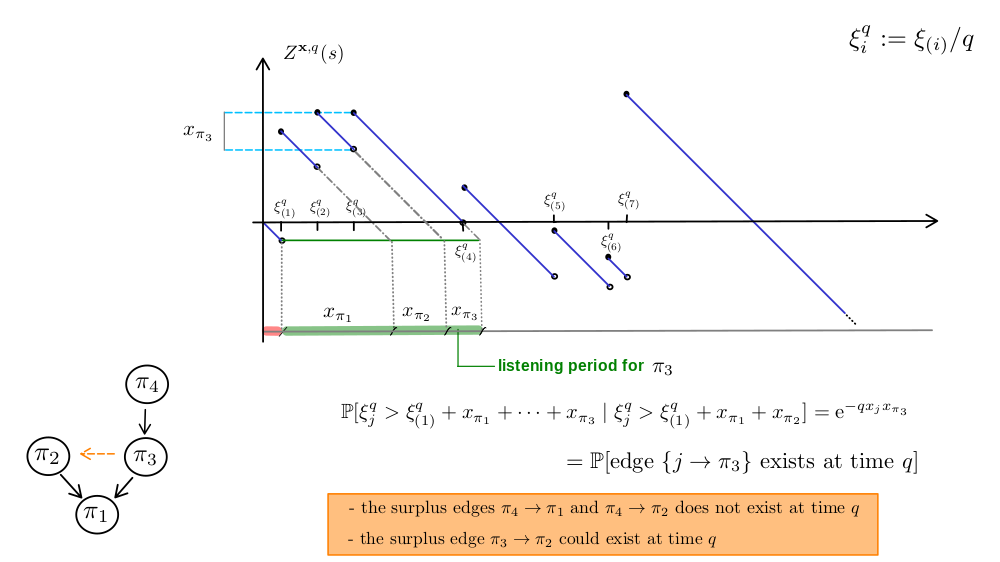
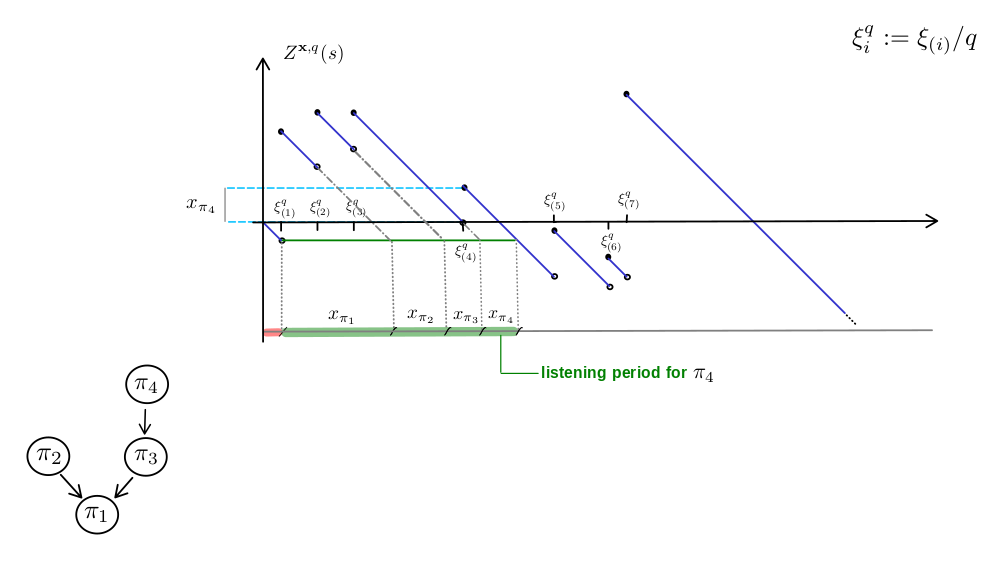
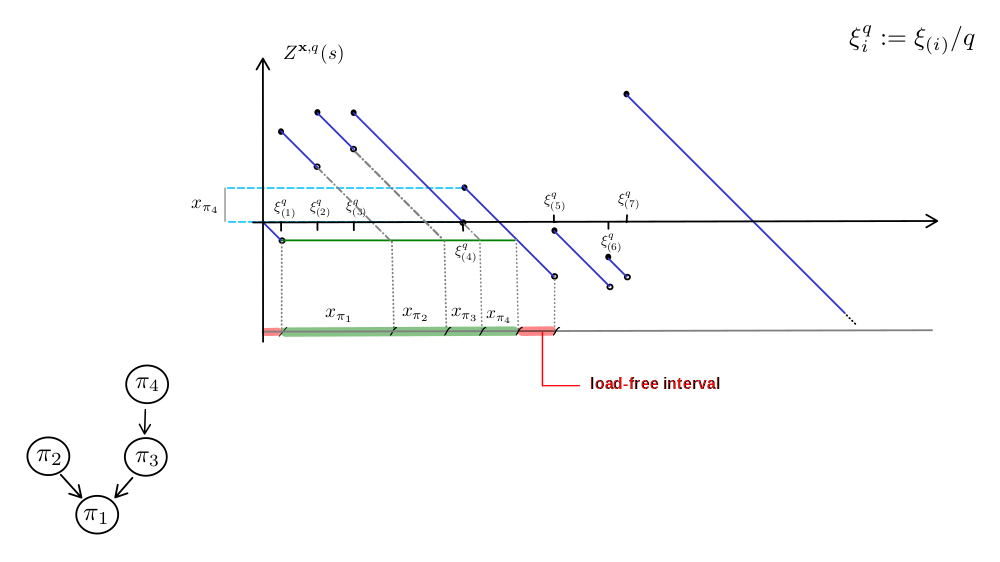
Erdös-Rényi random graph
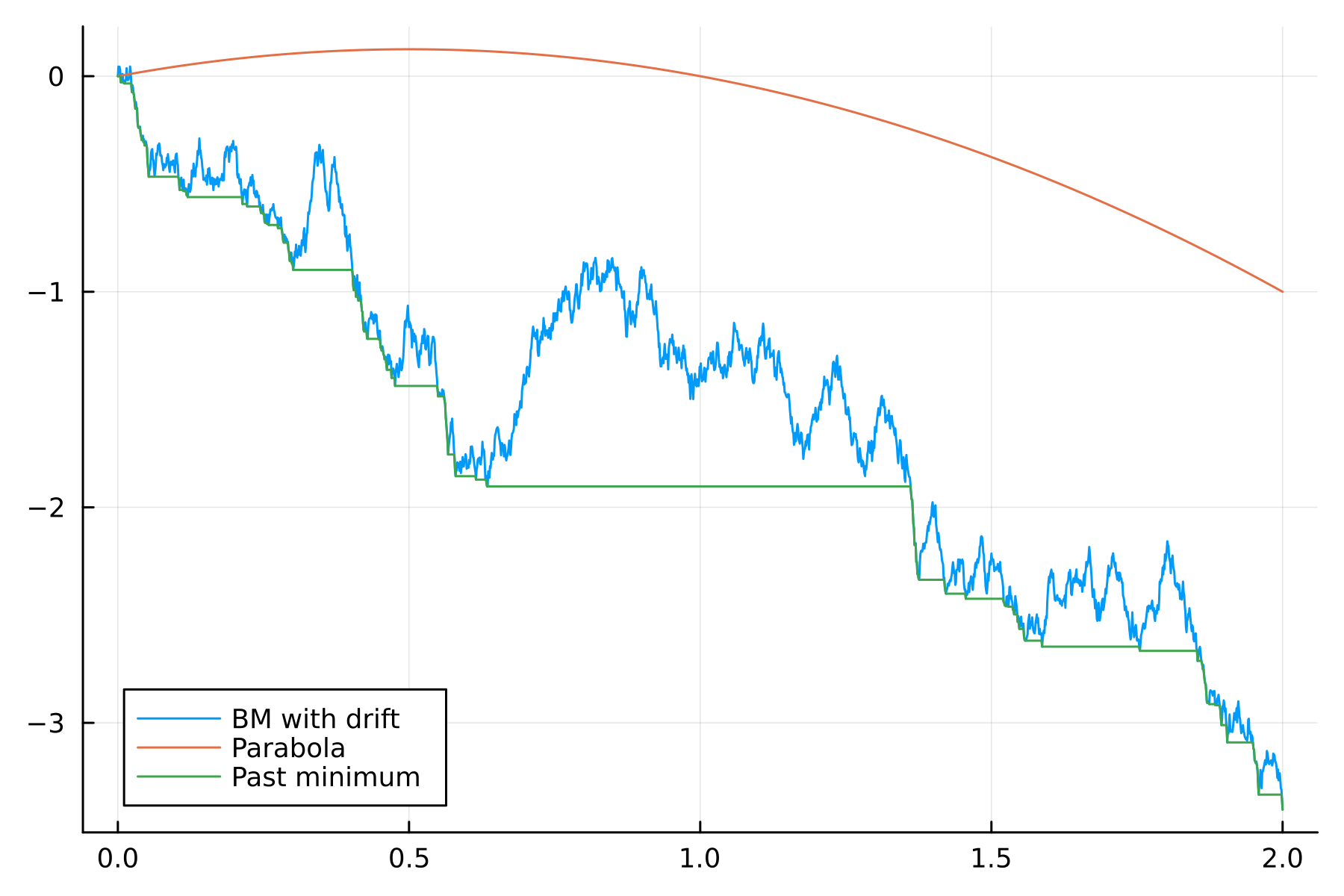
The limit process
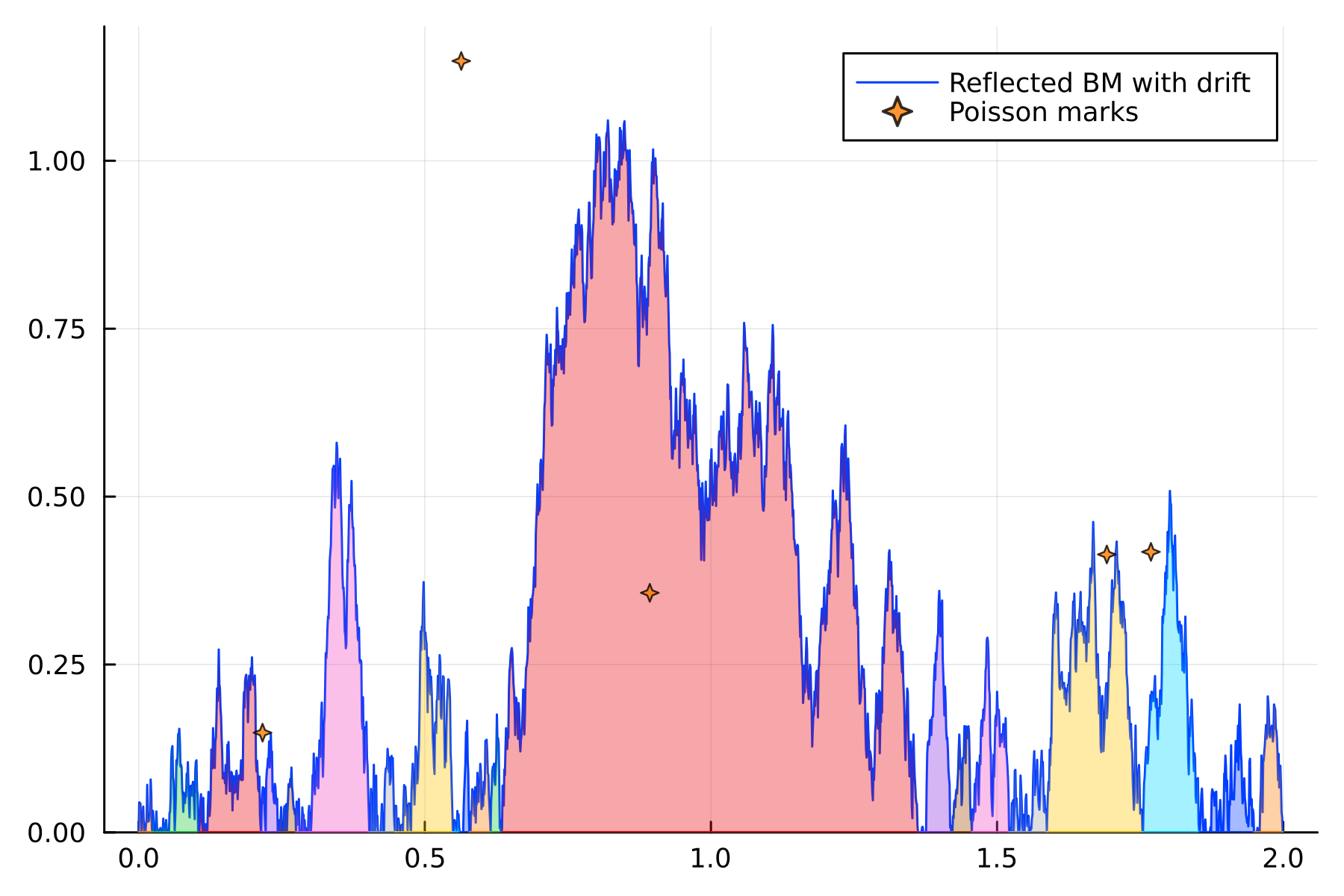
$$ B_t(s) = W_t(s) - \inf_{0 \leq u \leq s} W_t(u),$$where $ W_t(s) = W(s) - \frac{1}{2}s^2 + t s $.
-
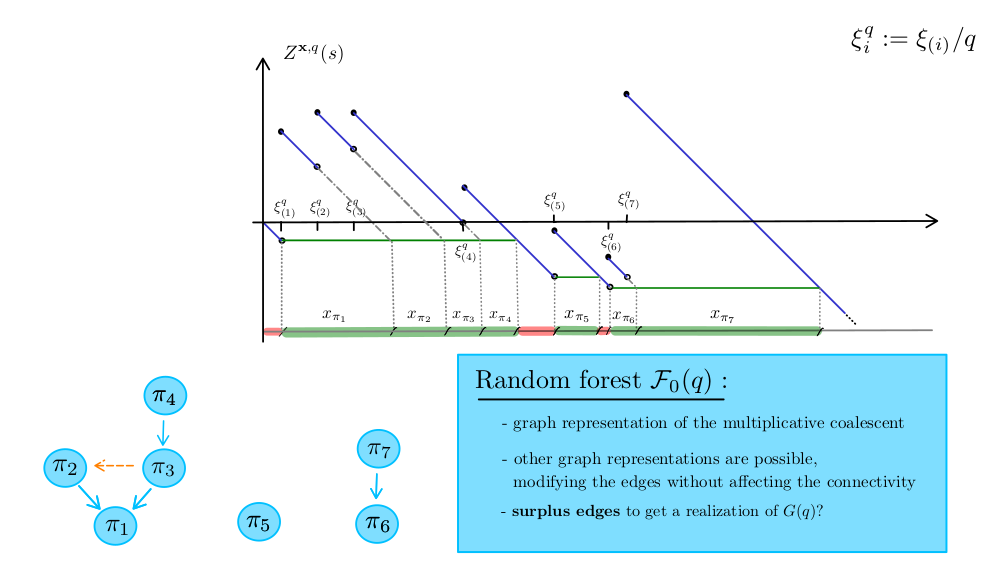
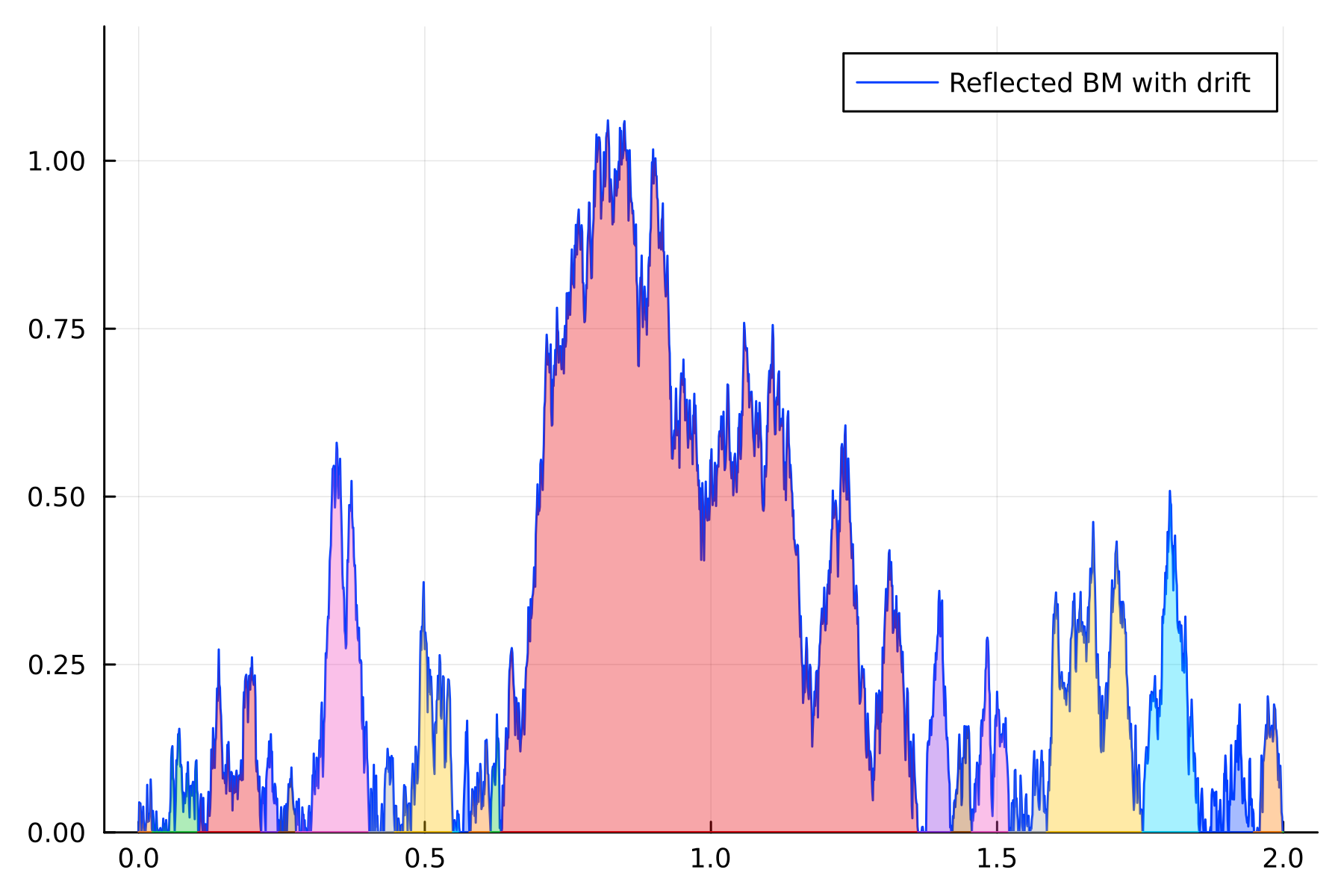
$X_i(t)$: $i$th largest excursion of $B_t(\cdot)$ above zero,
-
$\big( \pmb{X}(t), t \ge 0 \big) $ is a realization of an eternal multiplicative coalescent.
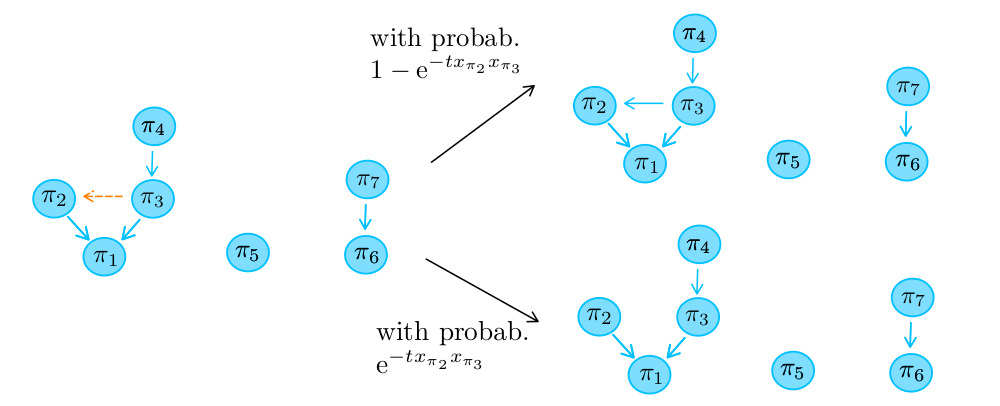
- $\Lambda$: homogeneous Poisson point process on $\mathbb{R}_+^2$,
- $X_i(t)$: $i$th largest excursion above zero,
- $Y_i(t)$: nb. of marks below the curve during the $i$th largest excursion.
$\big( (\pmb{X}(t), \pmb{Y}(t)), t \ge 0 \big) $ is a realization of an eternal augmented multiplicative coalescent.