A novel approach to the giant component fluctuations

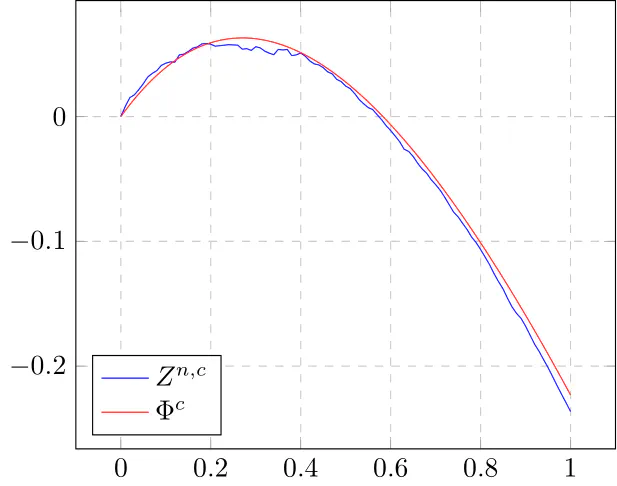
We present a novel approach to study the evolution of the size (i.e. the number of vertices) of the giant component of a random graph process. It is based on the exploration algorithm called simultaneous breadth-first walk, introduced by Limic in 2019, that encodes the dynamic of the evolution of the sizes of the connected components of a large class of random graph processes. We limit our study to the variant of the Erd\H{o}s,–,Rényi graph process $(G_n(s))_{s\geq 0}$ with $n$ vertices where an edge connecting a pair of vertices appears at an exponential rate 1 waiting time, independently over pairs. We first use the properties of the simultaneous breadth-first walk to obtain an alternative and self-contained proof of the functional central limit theorem recently established by Enriquez, Faraud and Lemaire in the super-critical regime ($s=\frac{c}{n}$ and $c>1$). Next, to show the versatility of our approach, we prove a functional central limit theorem in the barely super-critical regime ($s=\frac{1+t\epsilon_n}{n}$ where $t>0$ and $(\epsilon_n)_n$ is a sequence of positive reals that converges to 0 such that $(n\epsilon_n^3)_n$ tends to $+\infty$).

3